1.2.1 单重积分
考虑一个质点以速度v=v（t）运动，那么函数v（t）在区间t∈[a，b]上的积分，就是质点在时间区间[a，b]内所经过的路程。这个例子给出了定积分的物理意义。
设平面图形由曲线y=f（x）（f（x）≥0，x∈[a，b]），直线x=a，x=b以及x轴围成，如图1-1所示。那么f（x）在区间[a，b]上的积分就是此图形的面积，这个例子给出了定积分的几何意义。
图1-1 定积分示意图
1.2.2 多重积分
设想一个质量分布非均匀的不计厚度的平面薄板位于有界闭区域D上，面密度函数为μ=μ（x，y），那么μ在区域D上的二重积分就是平面薄板的质量。这个例子给出了二重积分的物理意义。
设z=f（x，y）是xy平面上有界闭区域D上的非负连续函数，其图形为曲面S。那么z=f（x，y）在区域D上的二重积分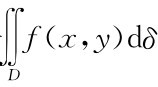
就是以区域D为底面，以D的边界为准线而母线平行于z轴的柱面为侧面、以曲面S为顶所形成的曲顶柱体的体积。这个例子给出了二重积分的几何意义，如图1-2所示。
图1-2 二重积分
如果二重积分的区域是y型正则区域，即
D=｛（x，y）|φ1（y）≤x≤φ2（y），c≤y≤d｝，其中：φ1，φ2∈C[c，d]，那么二重积分可以化成先对x后对y的累次积分，即
1.2.3 向量
既有大小又有方向的量称为向量，向量的大小称为模，模为1的向量称为单位向量。当且仅当两个向量的大小和方向都相同时，两个向量相等。如质点运动的速度，既有大小（速率）又有方向（运动方向），因此是一个向量；作用在质点上的力也是向量。
1.2.3.1 向量的数乘运算
对于实数λ和向量a，定义数乘向量是一个向量，记为λa。它的模是|λa|=|λ|·|a|，当λ＞0时，方向与a相同，当λ＜0时，方向与a相反。向量的数乘运算满足如下法则：
（1）1a=a；
（2）μ（λa）=（μλ）a；
（3）（μ+λ）a=μa+λa；
（4）λ（a+b）=λa+λb。
1.2.3.2 向量的加减法
设空间两个向量r1=x1i+y1j+z1k，r2=x2i+y2j+z2k，它们的和r1+r2=（x1+x2）i+（y1+y2）j+（z1+z2）k，它们的差r1-r2=（x1-x2）i+（y1-y2）j+（z1-z2）k。
在分子模拟中，如果要求一个原子受到的力，那么先要求作用在这个原子上所有的力，再用向量加法相加。
1.2.3.3 向量的内积和外积
两个向量的内积是一个标量，定义为r1·r2=|r1|·|r2|·cosθ，其中：θ为向量r1，r2之间的夹角。cosθ可以用余弦定理求得
所以r1·r2=x1x2+y1y2+z1z2。
它们的外积r1×r2是一个新向量，新向量的方向和向量r1，r2都垂直，且使r1， r2，r1×r2成右手系。新向量的模|r1×r2|=|r1|·|r2|·sinθ，其中：θ为向量r1，r2之间的夹角。新向量可以表示为r1×r2=（y1z2-z1y2）i+（z1x2-x1z2）j+（x1y2-y1x2）k。新向量的模是以r1，r2为边的平行四边形的面积。
1.2.4 矩阵、矩阵的特征值与特征向量
1.2.4.1 矩阵的运算
当且仅当两个矩阵有相同的行数和列数时，两个矩阵可以相加（减）。矩阵的和（差）等于两个矩阵中对应位置的元素分别相加（减）。设矩阵A=（aij）m×n，矩阵B=（bij）m×n，那么矩阵C=A+B=（aij+bij）m×n。仅当前一个矩阵的列数和后一个矩阵的行数相等的时候，两个矩阵可以相乘。设矩阵A=（aij）m×p，矩阵B=p （bij）p×n，那么它们的积C=AB=（cij）m×n，其中cij=Σaikbkj，i=1，2，…，m，j=1，2， k=1…，n。显然AB≠BA。
向量可以看成只有一行或者一列的矩阵，它们的加减和内积运算满足矩阵的加减和乘法法则。特别的，两个向量的外积可以表示成行列式的形式。对于向量
1.2.4.2 可逆矩阵
1.2.4.3 矩阵的特征值和特征向量
对于方阵A，最重要的性质是它的特征向量和特征值。如果存在非零向量x和实数λ，使得，Ax=λx，那么实数λ叫做矩阵的特征值，对应的向量x称为对应于特征值λ的特征向量。特征值和特征向量可以用如下方法计算：
Ax=λx⇒Ax=λx I⇒（A-λI）x=0。（A-λI）x=0成立的条件是x=0或者A-λI=0。根据定义，舍去x=0的解，计算行列式A-λI的值，令其等于0，可以得到关于λ的方程，解这个方程，可以得到方阵的特征值。通过特征值可以求得特征向量。如果A是一个实对称阵，那么它所有的特征向量都是实向量，并且相互正交（向量的内积为0）。通常情况下，对于高阶的矩阵，这种解方程的方法并不是求其特征向量和特征值的最佳方法，通常我们有多种数值方法可以求其特征向量。有兴趣的读者可以参考数值分析的相关教程。
1.2.5 数理统计的基本概念
随机变量的期望EX反映了随机变量X取值的“平均水平”。假如X表示寿命，则EX就表示平均寿命；假如X表示重量，EX就表示平均重量。从分布的角度看，数学期望是分布的中心位置。
X是一个随机变量，如果E（X-EX）2存在，则称E（X-EX）2为X的方差，记作DX，即DX=E（X-EX）2，称■DX为标准差或均方差。方差也可通过下式计算：DX=EX2-（EX）2。
（X，Y）是 二 维 随 机 变 量， 设 EX 和 EY 都 存 在， 如 果E[（X-EX）（Y-EY]）存在，则称其为随机变量X与Y的协方差，记作cov（X，Y），即cov（X，Y）=E[（X-EX）（Y-EY]）。
设X与Y为随机变量，如果EXk（k=1，2，…）存在，则称EXk为X的k阶原点矩，记为μk；如果E（X-EX）k（k=1，2，…）存在，则称E（X-EX）k为X的k阶中心矩，记为vk；如果E[（X-EX）k（Y-EY）l]存在，则称之为X与Y的k+l阶混合中心矩。
显然，X的数学期望EX是X的一阶原点矩，方差DX是X的二阶中心矩，协方差cov（X，Y）是X与Y的二阶混合中心矩。
一般地，设n维随机变量（X1，X2，…，Xn）的二阶中心矩
σij=E[（Xi-EXi）（Xj-EXj）] i，j=1，2，…，n
都存在，则称矩阵
为n维随机变量（X1，X2，…，Xn）的协方差阵。
为n维随机变量（X1，X2，…，Xn）的相关阵。
1.2.5.2 一些常见的分布
正态分布：一个连续型随机变量X，如果其密度函数为（-∞＜x＜+∞）。其中：μ，σ为常数，-∞＜μ＜+∞，σ＞0，则称X服从参数为μ和σ2的正态分布，记作X～N（μ，σ2）。数学期望EX=μ，方差DX=σ2。
χ2分布：设随机变量X1，X2，…，Xn相互独立，且Xi～N（0，1），则随机变量
服从自由度为n的χ2分布，记作χ2～χ2（n），其中n为正整数。
χ2（n）分布的分布密度函数为
t分布：设随机变量X～N（0，1），Y～χ2（n），且相互独立，则随机变量T=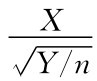
服从自由度为n的t分布（学生氏t分布），记作T～t（n）。其分布密度函数为
1.2.5.3 回归分析
回归分析是数理统计中处理变量之间相关关系的有力工具和常用方法。由一个或一组非随机变量来估计或预测某一个随机变量的值时，所建立的数学模型及所进行的统计分析，称为回归分析。
要考察两个变量X和Y之间的关系，就要研究Y的条件分布F（y|X=x）随X取值x的变化情况，但这一般是比较复杂的。作为一个近似，通常用F（y|X=x）的数学期望（平均值）来代替，通过研究x与Y的条件期望值y之间的关系来代表X与Y之间的关系。即
y=E（Y|X=x）=f（x）
y=f（x）就是X=x时随机变量Y的条件数学期望。在直角坐标系中它是一条普通的曲线，称为回归方程或回归曲线。
回归方程是一个确定性关系，其作用在于近似地代替了X与Y之间的相关关系，实质上是X与Y的平均值y之间的关系。利用回归方程，可以对y=E（Y|X=x）的取值进行预测和估计，也可以通过限制x的变化范围，使得y的值控制在一定范围内。
回归分析所建立的回归方程如果是线性的，则称为线性回归分析，线性回归分析根据自变量个数的多少，可分为一元线性回归和多元线性回归。
1）一元线性回归的模型
研究两个变量X与Y之间线性关系，建立其线性回归方程的统计分析方法称为一元线性回归。其一般模型为
Y=a+bx+ε
式中：E（Y|X=x）=a+bx，ε～N（0，σ2），即Y～N（a+bx，σ2）。这里x作为一般变量，Y是因变量，a，b称为回归方程的回归系数。
2）回归系数a，b以及方差σ2的估计
回归系数a和b的估计通常采用最小二乘法。设（xi，yi）（i=1，2，…，n）是X与Y的一组观测值，求解a和b的估计值＾a和＾b，使总的离差平方和
达到最小。由二元函数求极值的方法求解a和b的估计值。即
解得
3）多元线性回归模型
多元线性回归模型为Y=β0+β1x1+…+βmxm+ε，βi（i=0，1，2，…，m）是模型参数（回归系数），ε为随机变量，通常设ε～N（0，σ2）。进行n次观测，第i次的观测数据记为（yi；xi1，xi2，…，xim）（i=1，2，…，n）。若表示为矩阵形式：
则模型记为Y=Xβ+ε。当X可逆时，根据多元函数求极值的方法，回归系数的最小二乘估计为＾β=（X′X）-1X′Y。
上一篇：英文文本的语言特色
下一篇：宝宝的抓握反射也需锻炼
