
从几何的观点来看,产品设计的对象大部分是由回转面及螺旋面等函数曲面构成的三维实体。在现代汽车、航空航天、船舶等产品的设计中都要用到各种复杂的曲线和曲面,以实现产品外形设计的美观化和使用性能的优化,因此各种曲线和曲面在产品设计中非常重要。本节主要讨论曲线曲面的表示方法。
2.3.1 曲线模型
工程中应用的拟合曲线一般分为两种类型:一是最终生成的曲线通过所有的给定型值点,比如抛物样条曲线和三次参数样条曲线等,这类的曲线适用于插值放样;另一种曲线其最终结果并不一定通过给定的型值点,而只是比较接近这些点,这类曲线一般比较适合外形设计。此类曲线主要有Bezier曲线和B样条曲线。
1)Bezier曲线
Bezier曲线是通过一组折线集,或称为Bezier特征多边形进行定义的,曲线的起点和终点与该多边形的起点和终点重合,而且多边形的第一条边和最后一条边表示了曲线在起点和终点处的切向矢量方向。曲线的形状由特征多边形其余顶点控制,改变特征多边形顶点位置,可直观地看到曲线形状的变化。
(1)Bezier曲线的定义。Bezier构造曲线的基本思想是:由曲线的两个端点和若干个不在曲线的点来确定曲线唯一的形状。这两个端点和其他若干个点被称为Bezier特征多边形的顶点。
给定n+1个控制顶点Pi(i=0,1,…,n),可定义一条n次Bezier曲线:
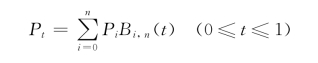
上式表示n+1阶(n次)Bezier曲线。其中,Pi为控制多边形的顶点;Bi,n(t)为伯恩斯坦(Bernstein)基函数,其定义为
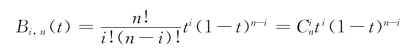
由于低阶Bezier曲线存在拼接连接性问题,而高阶Bezier曲线存在曲线摆动问题,所以工程上常用的是三次Bezier曲线。
三次Bezier曲线的基本形式为

其矩阵表示为

三次Bezier曲线实例如图2-11所示。
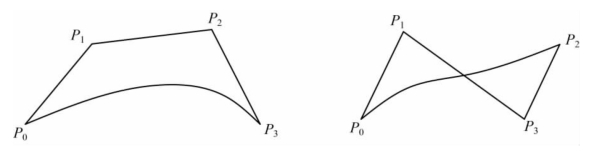
图2-11 三次Bezier特征多边形及曲线
(2)Bezier曲线的性质。
①端点性质。Bezier曲线的起点、终点与相应的特征多边形的起点、终点重合。Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条边的走向一致。
②对称性。假如保持n次Bezier曲线各顶点的位置不变,而把次序颠倒过来,此时曲线仍不变,只不过是曲线的走向相反而已。
③凸包性。Bezier曲线的形状由特征多边形确定,它均落在特征多边形的各控制点形成的凸包内。
④几何不变性。Bezier曲线的位置与形状仅与其特征多边形的位置有关,而与坐标系的选择无关。在几何变换中,只要直接对特征多边形的顶点变换即可,而无需对曲线上的每一点进行变换。
⑤全局控制性。当修改特征多边形中的任一顶点,均会对整体曲线产生影响,因此Bezier曲线缺乏局部修改能力。
2)B样条曲线
Bezier曲线有许多优越性,但有两点不足:一是控制多边形的顶点个数决定了Bezier曲线的阶次,并且在阶次较大时,控制多边形对曲线的控制将会减弱;二是Bezier曲线不能作局部修改,改变一个控制点的位置对整条曲线都有影响。
为了克服Bezier曲线存在的问题,1972年,Gordon、Rie-feld等人拓展了Bezier曲线。从外形设计的需求出发,希望新的曲线易进行局部修改,更逼近特征多边形,而且最好是低阶次曲线。于是,用B样条基函数代替了伯恩斯坦基函数,构造了B样条曲线的新型曲线。
(1)B样条曲线的定义。已知n+1个控制顶点Pi(i=0,1,…,n),可定义k次B样条曲线的表达式为
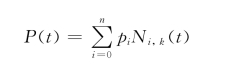
其中,Ni,k(t)为k次B样条基函数,可由以下的递推公式得到:
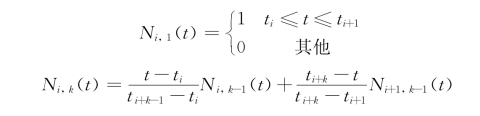
B样条曲线实例如图2-12所示。
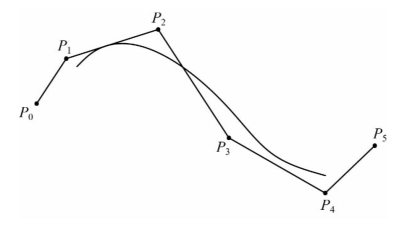
图2-12 B样条曲线及其控制多边形
(2)B样条曲线的性质。
①局部性。因为Ni,k(t)只在区间[ti,ti+1]中为正,在其他地方均取零值,使得k阶的B样条曲线在修改时只被相邻的k个顶点控制,而与其他顶点无关。当移动其中的一个顶点时,只对其中的一段曲线有影响,并不对整条曲线产生影响。局部性是B样条曲线最具魅力的性质。
②连续可导性。一般来说,k次B样条曲线具有k-1阶连续性。
③凸包性。B样条曲线比Bezier曲线具有更强的凸包性,比Bezier曲线更贴近特征多边形。
④几何不变性。B样条曲线的性质和位置与坐标系的选取无关。
⑤造型的灵活性。B样条曲线是一种非常灵活的曲线,曲线的局部形状受相应顶点的控制很直观。
(3)工程常用的三次B样条曲线。B样条曲线的阶次与控制点的数量无关,因此可任意增加控制点而不提高B样条曲线的阶次,这在工程应用中很重要。就阶次而言,曲线阶次的提高会使曲线更难控制和精准计算。因此,三次B样条曲线(即k=4)已能满足大多场合的应用需要。
对于n+1个特征多边形顶点P 0,P 1…Pn,每四个顺序点一组,其线性组合可以构成n-2段三次B样条曲线,即有4个控制点的三次B样条曲线。三次B样条曲线(n=3,k=0,1,2,3)的表达式为

如图2-13所示,三次B样条曲线段有如下的几何特征:
①端点位置矢量
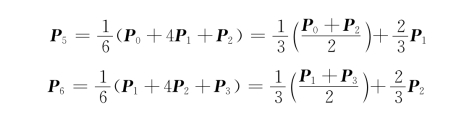
三次B样条曲线段的起点与终点分别位于△P0 P1P 2和△P1 P2 P3中线的三分之一处。
②端点切矢量
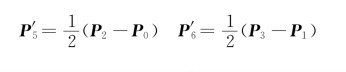

图2-13 三次样条曲线几何特征
曲线段起点与终点切矢量分别平行于P 0P 2、P 1P 3边,其模长为该边长的一半。所以,对三次B样条曲线相邻两段曲线,前一段曲线的终点就是后一段曲线的起点,而且对应共同的三角形,故两段曲线在连接点处具有相同的一阶导数矢量。
③端点的二阶导数矢量
P″5=P 0-2P 1+P 2=(P 0-P 1)+(P2-P1)
P″6=P1-2P2+P3=(P1-P2)+(P3-P2)
可见,曲线段起点和终点的二阶导数矢量等于特征多边形相邻两直线边所构成的平行四边形的对角线。由于三次B样条曲线上一段曲线终点处的平行四边形和下一段曲线在开始点处的平行四边形相同,所以三次B样条曲线在节点处有二阶连续导数。
2.3.2 曲面模型
曲面模型是计算机图形学的一项重要研究内容,主要研究在计算机图形系统环境下对曲面的表示、设计、显示和分析。工程设计中经常绘制各种曲面,曲面分为规则曲面与不规则曲面。规则曲面常见的有柱面、锥面、球面、环面、双曲面、抛物面等,这些曲面都可用函数或参数方程表示;而常见的不规则曲面有Bezier曲面、B样条曲面、孔斯曲面等,这些曲面采取分片的参数方程来表示。
不规则曲面的基本生成原理是:先确定曲面上特定的离散点(型值点)的坐标位置,通过拟合使曲面通过或逼近给定的型值点,得到相应的曲面。一般情况下,曲面的参数方程不同,就可以得到不同类型及特性的曲面。
1)Bezier曲面
Bezier曲面是Bezier曲线的拓广。用一个参数t描述的向量函数可以表示一条空间曲线,而用两个参数u、v描述的向量函数就能表示一个曲面。
设有控制点Pij(i=0,1,2,…,m;j=0,1,2,…,n)为(m+1)×(n+1)个空间点列,则可定义一个m×n次Bezier曲面
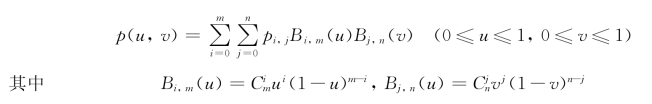
为伯恩斯坦基函数。依次用线段连接点列Pij(i=0,1,2,…,m;j=0,1,2,…,n)中相邻两点所形成的空间网格称为Bezier曲面的特征多边形网格。
当m=n=3时,双三次Bezier曲面由16个控制网格点构造,如图2-14所示。
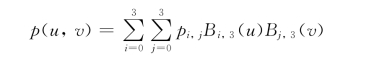
从图2-14中可以看出曲面通过特征网格的四个角点;曲面中的曲线u和曲线v均为Bezier曲线;曲面落在特征网全体顶点的凸包内。另外,Bezier曲线的性质都可以推广到Bezier曲面,如对称性、几何不变性和全局控制性等。
2)B样条曲面
B样条曲面同样也是B样条曲线的拓广。通用B样条曲面方程为:给定(m+1)×(n+1)个控制点Pij(i=0,1,2,…,m;j=0,1,2,…,n),可定义k×l次B样条曲面
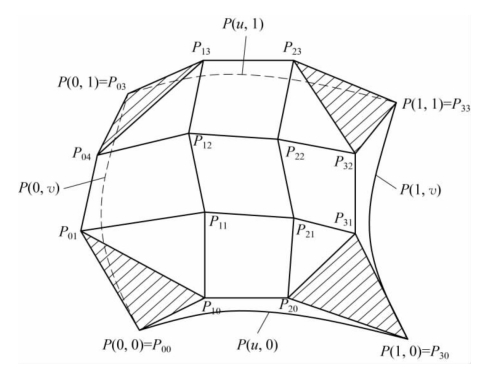
图2-14 双三次Bezier曲面片及边界信息
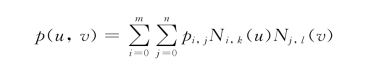
式中,Ni,k(u)和Nj,l(v)分别为k次和l次B样条基函数,由控制点Pij组成的空间网格称为B样条曲面的特征网格。
如图2-15所示,对于k=l=3,双三次B样条曲面方程为
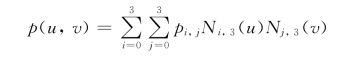
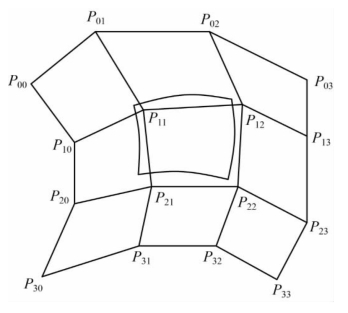
图2-15 双三次B样条曲面片
由图2-15可以看出,k×l次B样条曲面片的四个角点不经过任何特征网格顶点,且仅与该角点对应的k×l个特征网格顶点有关;B样条曲面的边界曲线仍为B样条曲线,该边界B样条曲线由对应的k条(或l条)边界特征网格顶点确定。而且B样条曲面也具有几何不变性、对称性和凸包性。B样条曲面边界的跨界导数只与定义边界的顶点及相邻k-1排(或l-1排)顶点有关,具有(k-1)×(l-1)阶函数连续性。这是由三次B样条基函数族的连续性保证的。所以,双三次B样条曲面的突出特点就在于相当轻松地解决了曲面片之间的连接问题。







