
图3.10
从图3.11可以看出,如果曲线y=f(x)是凹(凸)的,则其上各点处的切线斜率随x的增加而增加(减少),所以f′(x)是x的单调增加(单调减少)函数.如果f(x)二阶可导,那么用二阶导数的符号就能确定一阶导数的单调性,从而有以下定理:
图3.11
定理1 设f(x)在[a,b]上连续,在(a,b)内具有二阶导数.
(1)如果在(a,b)内f″(x)>0,则曲线y=f(x)在[a,b]上是凹的;
(2)如果在(a,b)内f″(x)<0,则曲线y=f(x)在[a,b]上是凸的.
例1 讨论曲线y=x3的凹凸性.
解 函数y=x3的定义域为(-∞,+∞).
y′=3x2,y″=6x.
当x<0时,y″<0,所以曲线在(-∞,0]上是凸的;当x>0时,y″>0,所以曲线在[0,+∞)上是凹的.
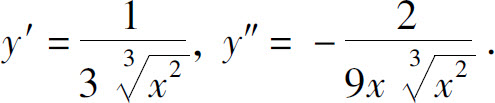
当x=0时,y′,y″都不存在.
当x<0时,y″>0,所以曲线在(-∞,0]上是凹的;当x>0时,y″<0,所以曲线在[0,+∞)上是凸的.
定义2 如果连续曲线y=f(x)在点(x0,f(x0))两侧的凹凸性不同,则称点(x0,f(x0))为曲线的拐点.
由定理1可知,在拐点的两侧f″(x)必然异号.故而在拐点处f″(x)=0或f″(x)不存在.
例3 求曲线y=ln(1+x2)的凹凸区间及拐点.
解 函数y=ln(1+x2)的定义域为(-∞,+∞).
令y″=0,解得x1=-1,x2=1.
x1=-1,x2=1把函数的定义域(-∞,+∞)分成三个部分区间:
(-∞,-1],[-1,1],[1,+∞).
在(-∞,-1)内,y″<0;在(-1,1)内,y″>0;在(1,+∞)内,y″<0.因此曲线的凹区间为[-1,1];曲线的凸区间为(-∞,-1],[1,+∞).
当x=-1时,y=ln2,点(-1,ln2)是这曲线的一个拐点;当x=1时,y=ln2,点(1,ln2)也是这曲线的拐点.
定义3 当曲线C上的动点P沿着曲线C无限延伸时,如果动点P到某直线l的距离趋近于0,则称直线l为曲线C的渐近线,如图3.12所示.
图3.12
曲线的渐近线有两种:垂直渐近线和斜渐近线(包括水平渐近线).
所以,直线x=0与x=-1都是曲线的垂直渐近线.
如图3.12所示,设直线y=ax+b是曲线y=f(x)的斜渐近线,下面讨论怎样确定常数a和b.
由点到直线的距离公式,曲线y=f(x)上点(x,f(x))到直线y=ax+b的距离
因为直线y=ax+b是曲线y=f(x)的斜渐近线,故
函数图形是函数的直观表示.借助于函数图形可以直观地反映函数的变化规律和性状,有助于对函数进行深入研究.
利用导数描绘函数图形的一般步骤如下:
(1)确定函数y=f(x)的定义域,考察函数有无奇偶性与周期性.
(2)求f′(x)和f″(x).
(3)求出f′(x),f″(x)在定义域的全部零点,并求出f(x)的间断点以及f′(x),f″(x)不存在的点.用这些点将函数的定义域划分为若干个部分区间.
(4)确定在这些部分区间内f′(x)和f″(x)的符号,并由此确定函数图形的升降、凹凸和拐点,以及函数的极值点.
(5)确定函数图形的渐近线.
(6)算出第(3)步所得各分点处的函数值,确定出图形上的相应点.为了把图形描绘得准确些,有时还需要补充一些点.然后结合第(4)和第(5)步中的结果,连接这些点画出函数y=f(x)的图形.
解 (1)所给函数的定义域为(-∞,+∞),由于
所以函数f(x)是偶函数,它的图形关于y轴对称.因此可以只讨论[0,+∞)上该函数的图形.
(2)求导:
(3)在[0,+∞)上,方程f′(x)=0的根为x=0;方程f″(x)=0的根为x=1.用点x=1把[0,+∞)划分成两个区间:[0,1],[1,+∞).
(4)对单调性、凹凸性、极值和拐点列表讨论.
(5)由于 ,所以图形有一条水平渐近线y=0.
,所以图形有一条水平渐近线y=0.
(6)计算x=0,1处的函数值:
图3.13
解 (1)所给函数的定义域为(-∞,1)∪(1,+∞).
(2)求导:
(3)令y′=0得x1=-1,x2=3.这两个点把定义域划分为
(-∞,-1],[-1,1),(1,3],[3,+∞).
(4)对单调性、凹凸性、极值和拐点列表讨论.
(5)由例3知有垂直渐近线x=1及斜渐近线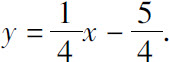
(6)根据上述讨论,连接相关点可描绘出函数的图形,如图3.14所示.
图3.14
1.求下列曲线的凹凸区间和拐点:
(1)y=3x-2x2;
(3)y=x3-6x2+3x;
(4)y=xe-x;
(5)y=(x+1)4+ex;
2.已知曲线y=x3+ax2-9x+4x在x=1处有拐点,试确定系数a,并求曲线的拐点和凹凸区间.
3.问a,b为何值时,点(1,3)为曲线y=ax3+bx2的拐点?
4.求下列曲线的渐近线:
5.描绘下列函数的图形:
(1)y=2x3-3x2;
(2)y=x4-6x2+8x;
(4)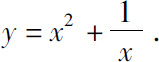
上一篇:以租赁方式租入的固定资产
下一篇:浙江省船舶产业竞争力发展报告







