
第5章介绍了用傅里叶变换分析线性动态电路的概念。傅里叶变换要求原函数f(t)满足绝对可积条件。这个条件是十分苛刻的,工程中常用的阶跃函数和正弦函数等都不满足这个条件。
研究动态电路暂态过程时,激励函数f(t)都是在t=0时开始作用的,即t <0,f(t)=0,这类函数称为因果函数或有始函数。可取负指数函数e-σt去乘f(t),则得函数g(t)
![]()
式中σ是正实数。只要σ足够大,对于实际上遇到的大多数函数f(t),总可做到使g(t)是绝对可积的,即

因此,对函数g(t)可进行傅里叶变换。因为t<0时,f(t) =0,g(t) =0,所以傅里叶积分的下限从零开始,成为单边傅里叶变换,即

令σ+jω=s,称为复频率,则式(7-3)可写为
式(7-4)称为拉普拉斯变换。F(s)称为f (t)的象函数,而f(t)称为F(s)的原函数。式(7-4)可简记为
对F(σ+jω)进行傅里叶反变换,则得
以g(t)=f(t)e-σt代入式(7-6),等式两边同乘eσt得
因为s= σ+jω,dω=ds/j,相应于ω的上下限±∞ ,s的上下限为σ±j∞。把这些关系代入式(7-7),则得

式(7-8)是拉普拉斯反变换,与式(7-4)构成一个变换对。式(7-8)可简记为
![]()
本章采用拉普拉斯变换法,把时域中求解原函数的微分方程转化为复频域中求解象函数的代数方程,使运算大大简化。这种方法称为复频域分析法或运算法。
下面利用式(7-4)计算几个常见时间函数的象函数,其他一些常用函数的象函数列于表7-1中。
表7-1 常见的拉普拉斯变换

1.单位阶跃函数的象函数
若f(t)=ε(t),则
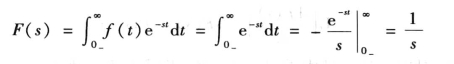
2.单位冲击函数的象函数
若f(t)=δ(t),则

3.指数函数的象函数
若f(t)=e-at,则
同理,若f(t)=eat,则F(s)=1/(s-a)。
上一篇:莫斯科地铁号线
下一篇:胡夫金字塔的建造历史







