极限定理与中心极限定理

极限定理_统计学教程

    第三节　极限定理

    极限定理是采用极限的方法求得随机变量分布的一系列定理。极限定理内容广泛，一般可分为两类：一类阐述什么条件下，可以将概率接近0的事件或概率接近1的事件分别看做“实际上的不可能事件”或“实际上的必然事件”，有关这一类极限定理的命题，统称为大数定律；另一类极限定理阐述在怎样的条件下，当n→∞时，独立随机变量之和的极限分布为正态分布，有关这一类极限定理的命题，统称为中心极限定理（Central limit theorem）。

    一、大数定律

    概率的统计定义利用的是事件发生的频率具有稳定性这一特征，即随着试验次数的增加，事件发生的频率逐渐稳定于某个常数。在实践中大量测量值的算术平均数也具有这种稳定性。下面定理反映算术平均数的稳定性。

    定理：　设随机变量X₁，X₂，…，X_n，…相互独立，并具有相同的数学期望和方差：E（X_k）＝μ，V（X_k）＝σ²（k＝1，2，…），且有

    

    则对于任意正数ε有

    

    定理表明，当n很大时，期望值相等的独立随机变量的算术平均数接近于它们的期望值。

    二、中心极限定理

    中心极限定理是大样本统计推断的理论基础。在实际问题当中，有许多随机变量是由大量相互独立的随机因素综合而成的，因此它们都可以表现为大量的随机变量之和。中心极限定理就是一系列关于随机变量之和的分布在怎样的条件下渐进服从正态分布的定理。这里主要介绍三个定理。

    定理一（独立同分布的中心极限定理）：设随机变量X₁，X₂，…，相互独立，服从同一分布，并具有相同的数学期望和方差：E（X_k）＝μ，V（X_k）＝σ²≠0（k＝1，2，…，n），则随机变量

    

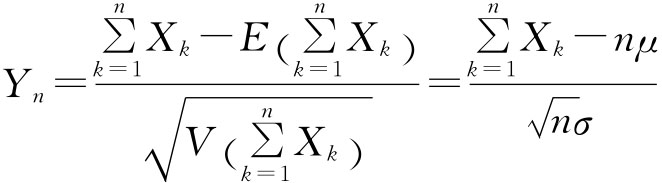
    的分布函数F_n（x）对于任意x满足

    

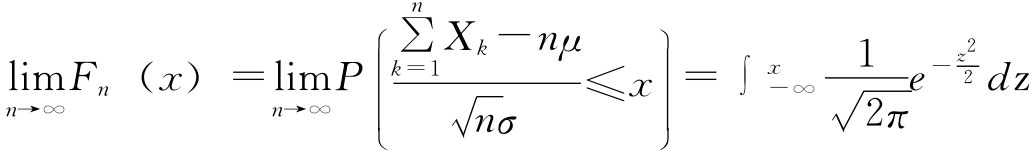
    定理二（Liapunov定理）：设随机变量X₁，X₂，…，X_n相互独立，具有数学期望和方差：E（X_k）＝μ_k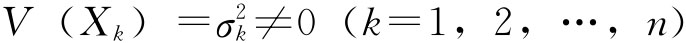，，记

    

    若存在正数δ，使得当n→∞时，

    

    则随机变量

    

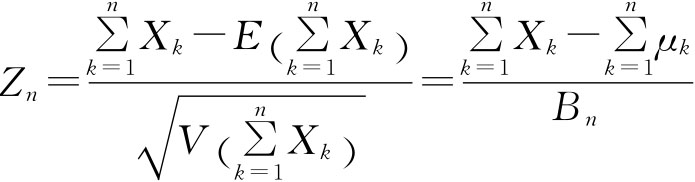
    的分布函数F_n（x）对于任意x，满足

    

    定理表明，无论各个随机变量X_k（k＝1，2，…，n）服从什么分布，只要满足定理的条件，当n很大时，它们的和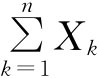就近似服从正态分布。

    例4－6：根据以往经验，某种电器元件的寿命服从均值为100小时的指数分布，现随机抽取16只，它们的寿命可看做是相互独立的，计算这16只元件的寿命总和大于1920小时的概率。

    解：设X_k表示该种电器元件的寿命，则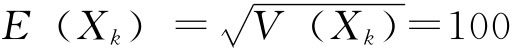

    

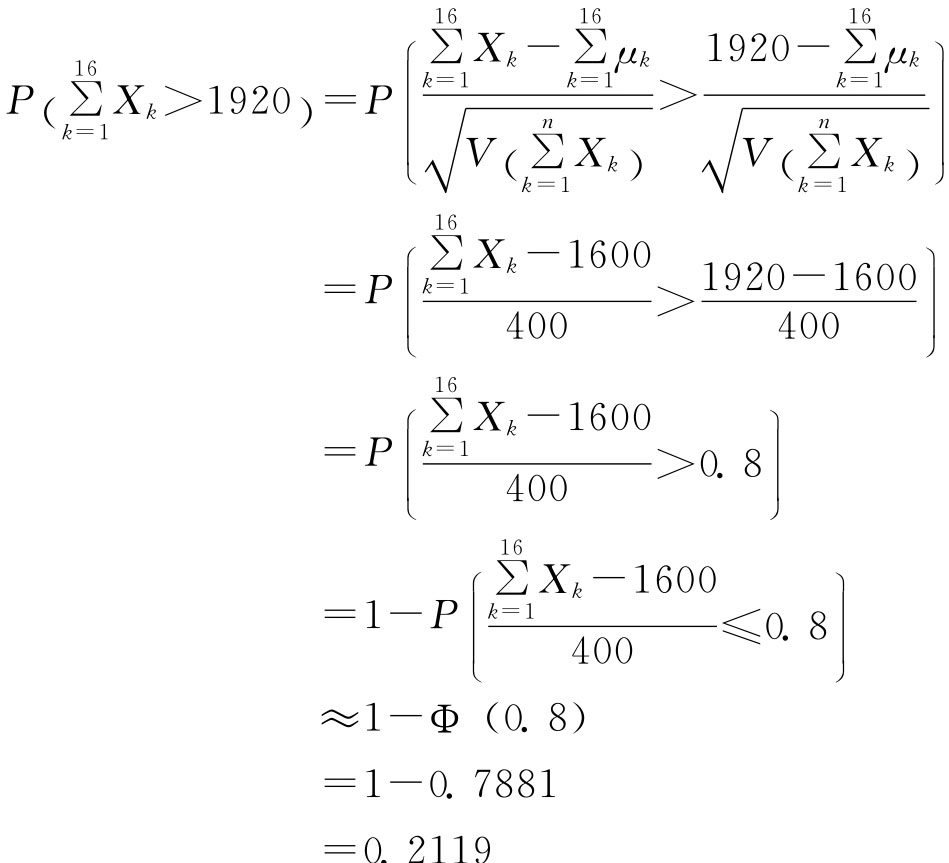
    即这16只元件的寿命总和大于1920小时的概率为21.19%。

    定理三（De Moivre－Laplace定理）：设随机变量η_n（n＝1，2，…）服从参数为n，p（0＜P＜1）的二项分布，则对于任意x，恒有

    

    这个定理表明，正态分布是二项分布的极限形式，当n充分大时，可利用该定理的结论计算二项分布的概率。

    例4－7：抽样检查产品质量时，如果发现次品数多于10件，则认为这批产品不能接受，问应检查多少件产品，可使次品率为10%的一批产品不被接受的概率达到90%？

    解：

    

    

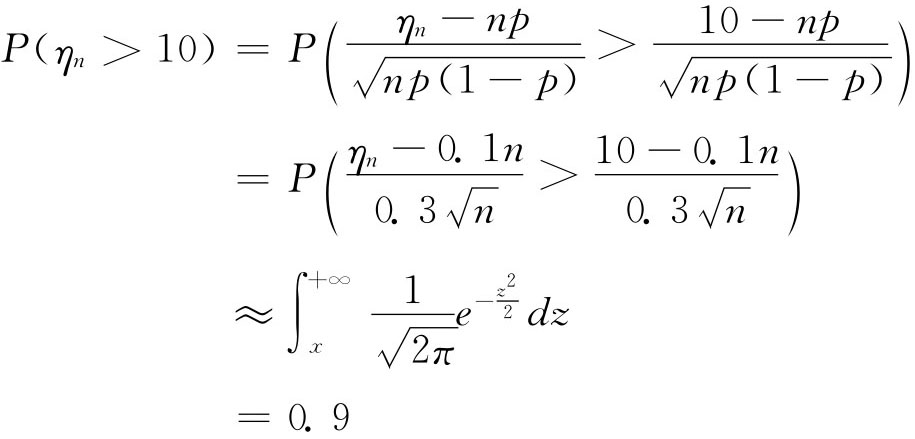
    n＝146

    即应检查146件产品可使这批次品率为10%的产品不被接受的概率达到90%。