
移动平均线被称为数据平滑器,其作用就是平滑时间域内的波形。移动平均线移除了输入数据中的短期的弯曲曲线,通过和周期一起发挥作用,比普通的平滑器更有优势,放置移动平均线更精确。因为移动平均线是低通滤波器的一种形式,短期的弯曲曲线是由复合波形中的高频组成波产生的,所以这些曲线会被移除。低通滤波器只允许低频组成波通过,并且不会被衰减,而阻拦高频组成波的通过。我们的分析描述了这是如何被完成的,以及使用低通滤波器会产生哪些纷繁复杂而又难以预料的结果。
一般来说,低通滤波器有两种:有限脉冲响应滤波器和无限脉冲响应滤波器。简单移动平均线(SMAs)是一种有限脉冲响应滤波器。有限脉冲响应滤波器之所以这样命名,是因为如果我们输入一个短的峰值,滤波器产生的结果就会显示只有有限脉冲响应滤波器窗口的长度。因此,滤波器在时间长度中对脉冲的响应是有限的。指数移动平均线(EMAs)是一种无限脉冲响应滤波器。无限脉冲响应滤波器使用卷积的计算来获得过滤后的输出。也就是说,当前输出不仅仅是当前输入的结果,还是前面输出计算的结果。理论上,既然计算是卷积的,那么任何输入都会永远显示在输出中。
滤波器的滞后特性很可能对交易者有较大的冲击(影响),远远比它可以达到的平滑效果的影响更严重。很容易看到,一条简单移动平均线的滞后大约是滤波器长度的一半。既然输出代表了一个在滤波器的水平中心的附近值,且这个滤波器有N根价格柱的长度,简单移动平均线的滞后就刚好是(N-1)/2根柱状线。工程师将滤波器滞后组称为“延迟”(Delay)。他们将组延迟和相位的延迟区别开来,为了更好地区分这些不同延迟,我们需要考虑波的速度。
画出一个涌上沙滩的海浪。组速度是波在和波浪正交方向上的波速。如果这些波以45°的角度拍打海岸,相位速度就是波运行到海岸的峰值的速度。一个真实世界的滤波器的例子是飞机雷达天线罩。天线罩能够识别雷达频率,但不传导其他的无线电频率。因此,雷达天线罩就是一种滤波器。组速度不能超过光速,因为这是能量传播的速度。在另一方面,相位速度可以非常大。
回到与交易相关的滤波器,下面来分析一条2根柱状线的简单移动平均线。群延迟是滤波器的中间值,或者0.5根柱状线的延迟。相位延迟随着频率线性变化。相位延迟在频率为0时是0。角度频率是2π乘以真实频率,因为每个周期完成了2π弧度。市场数据是抽样的数据,并且抽样理论要求每个周期必须至少有两个样本。这个最高可能的频率被称为奈奎斯特频率(Nyquist frequency)。例如,奈奎斯特频率为0.5周期每根柱状线。既然我们常常用周期长度来表示奈奎斯特周期,而不是它的倒数,那么我们应该说奈奎斯特周期是长度为2根柱状线的周期。抽样数据系统的结果常常标准化到奈奎斯特频率的形式。图4.1显示了一条2根柱状线简单移动平均线的波幅和相位输出。滤波器输出波幅以十进制(20×log(波幅))表示。
图4.1显示了一个2根柱状线周期几乎就被消除了,因为每个周期中的两个样本的平均值为0。画出来的相位显示了相位是频率的函数。周期长度为2除以标称化的频率。因此,对一个5根柱状线周期,标称化的频率就是0.25。
图4.1 2根柱状线简单移动平均线的频率和相位响应
在2根柱状线移动平均线中,5根柱状线的周期就有25°的相位延迟。类似的,一个3根柱状线的周期(标称化频率=0.667)有60°的相位延迟。
组延迟有一个基础的定义,就是相位对应于角度频率的改变速度。在所有频率里面,2根柱状线简单移动平均线的相位,其改变速度是恒定的。这个速度可以被计算,公式就是在奈奎斯特频率(π/2)的相位除以奈奎斯特频率(2×π×0.5)的角度。做完除法,我们看到组延迟是0.5根柱状线,刚好与我们从滤波器长度考量中计算出来的(N-1)/2的延迟一样。这个延迟的计算是对延迟更基本的定义,因为它也适用于无限脉冲响应滤波器。
图4.2显示了2根柱状线周期和4根柱状线周期都几乎被4根柱状线简单移动平均线消除了。
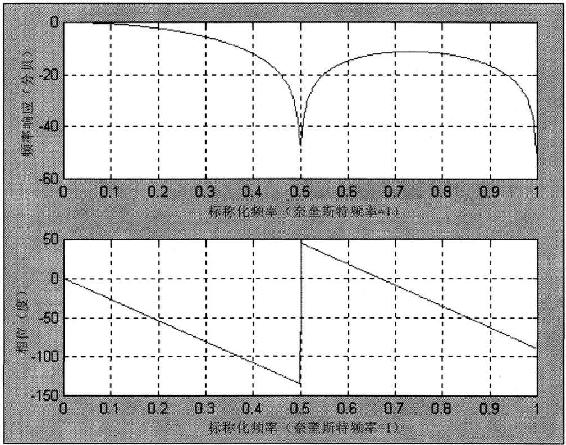
图4.2 4根柱状线简单移动平均线的频率和相位响应
滤波器的相位响应和在波幅为0时相隔了90°,但是除了在频率为0时,相位的改变速度都是线性的。在奈奎斯特角度频率为π时,总的相位移动为3π/2,就像相位改变速度计算出的1.5根柱状线滞后一样。滞后对所有频率都是恒定的。
将简单移动平均线的长度再次乘以2,我们在图4.3中看到了一个8根柱状线简单移动平均线的表现。2、8/3、4、8根柱状线周期都被滤波器过滤掉了,因为每一个周期都是滤波器长度的整数倍,都是周期长度的整数,导致这些周期在滤波器中的平均值为0。奈奎斯特频率的总相位滞后是7π/2,因此通过这个滤波器产生的滞后就是3.5根柱状线。
图4.3 8根柱状线简单移动平均线的频率和相位响应
加权移动平均线(WMA)是一个有限脉冲响应滤波器。它和简单移动平均线类似,除了滤波器的系数被加权,与滤波器中数据的新旧程度成反比,并且被标称化为系数的总和。在“易语言”编程中,变量后的[N]表示使用N根柱状线之前的变量。因此,加权移动平均线可以写为
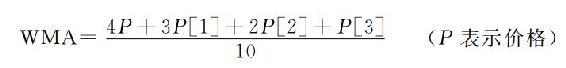
4根柱状线加权移动平均线的频率和相位响应显示在图4.4中。因为加权移动平均线有不对称的加权系数,所以没有区别的频率从滤波器中被移除了。另外,相位响应不是线性的,意味着不是所有频率的组延迟都是恒定的。4根柱状线加权移动平均线的组延迟显示在图4.5中。
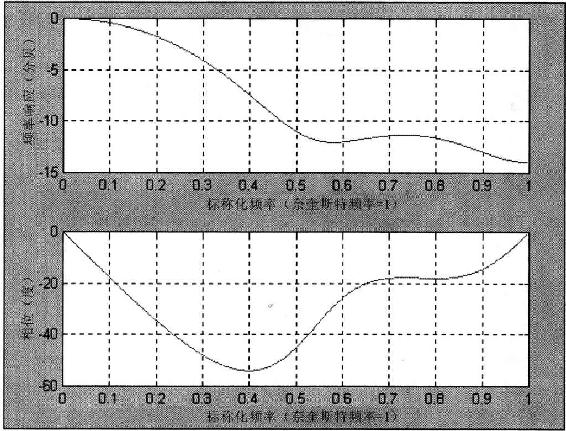
图4.4 4根柱状线加权移动平均线的频率和相位响应
加权移动平均线的系数,形成了一个穿过滤波器宽度的三角形轮廓。一个有效脉冲响应滤波器的重要低频滞后可以从被描述为滤波器系数的几何形态“引力中心”推测。既然加权移动平均线系数的几何形态是一个三角形,低频滞后可以通过表达式(N-1)/3推测,因为这是三角形的重心,那么,对于4根柱状线加权移动平均线,低频滞后就是1根柱状线。这刚好对应显示在图4.5中的低频组延迟。已经被衰减的频率组成的滞后关系不大,因为与输入波幅相比,它们的(输出)波幅是很小的。
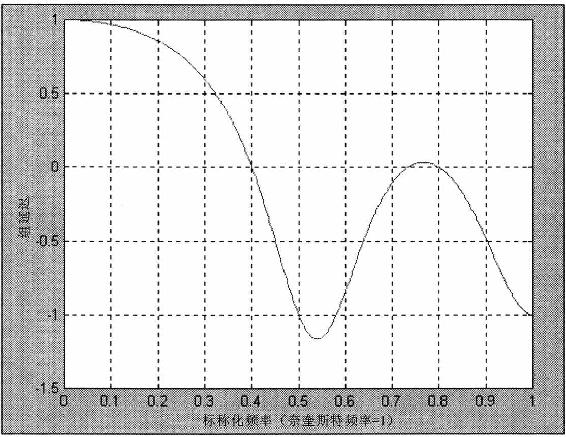
图4.5 4根柱状线加权移动平均线的组延迟
一些对称的有限脉冲响应滤波器对交易者是有用的,因为它们剔除了可能在市场数据中存在的特定的频率组成。例如,4根柱状线对称有限脉冲响应滤波器的系数(FIR)为
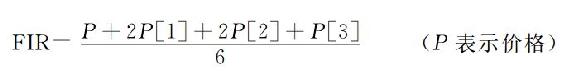
这个滤波器有一个频率响应,如图4.6所示。这个滤波器刚好就剔除了2根柱状线和3根柱状线的周期。它对所有的频率有一个1.5根柱状线的延迟。
衍生到6根柱状线的对称的有限脉冲响应滤波器,系数如下
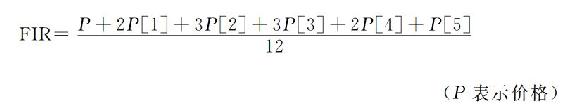
这个滤波器有一个频率响应,如图4.7所示,刚好就剔除了2、3、4根柱状线的周期。
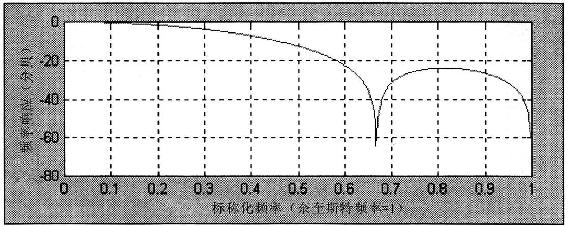
图4.6 一个对称4根柱状线有限脉冲滤波器的频率响应
另外,除了可以剔除有一个整数的柱状线长度的周期,滤波器对在这些整数柱状线周期之间的频率组成部分有明显的衰减作用。对所有的频率有2.5根柱状线滞后。
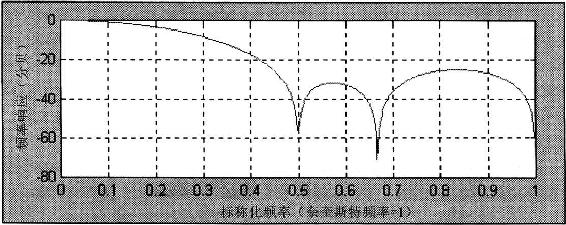
图4.7一个对称6根柱状线有限脉冲响应滤波器的频率响应
我们已经讨论过的有限脉冲响应滤波器是非卷积的。也就是说,我们没有使用前面的计算结果来计算当前的移动平均线的值。无限脉冲响应滤波器在方法上的主要不同,就是它们是卷积的。指数移动平均线是交易者最熟悉的无限脉冲响应滤波器。在指数移动平均线中,计算使用了当前价格的一部分加上另一个滤波器的计算结果,比如1根柱状线前的部分。第一个部分被称为阿尔法(α),并且其取值范围为0到1。两个部分的和必须等于1,所以第二个部分的值就是1减去α。计算指数移动平均线的公式为
EMA=αP+(1-α)×EMA[1]
指数移动平均线从左往右穿过价格数据,从一根柱状线移动到下一根,从而达到移动平均的效果。通常把指数移动平均线写成代码,确保α和(1-α)的和等于1。如果两个数的和不等于1,那么滤波器的输出就是错误的,并且这个错误可能会一直增加,直到使计算机崩溃。
指数式这个词描述了指数移动平均线传递波幅上的响应相对于单个输入的波幅衰减。设想一个情况,数据组里面的第一根柱状线的波幅为1/α,并且后面的波幅在各个地方都为0。当指数移动平均线被应用到这个数据上,滤波器的第一个输出就是1,因为指数移动平均线没有前值。在后面的计算中,价格的值还是0,并且计算的顺序就是(1-α)的高阶指数乘以前面的计算值。因此,当指数增加,输出的波幅下跌。
α与简单移动平均线的长度的关系如下:
α=2/(长度+1)
我喜欢把指数移动平均线的α看作一个滞后,即直接影响交易指标和系统上的指数移动平均线的滞后。既然这个滞后大约就是一半的简单移动平均线的长度,那么α就可以这样计算:
α=1/(滞后+1)
对一个8根柱状线简单移动平均线来说,α=0.222。使用这个α的频率和相位响应显示在图4.8中。
这个响应可以和图4.3中的8根柱状线简单移动平均线的频率和相位响应进行比较。在频率响应中没有尖锐的陷波,因为卷积的计算排除了任何给定频率的组成波的抵消作用。相位延迟是非线性的,因此,不是任何频率的组延迟(滞后)都是恒定的。指数移动平均线的组延迟显示在图4.9中。注意,3.5根柱状线的低频滞后刚好和简单移动平均线的滞后相同,但是当频率增加时,滞后快速下降。滞后随着频率的增加而减少,是指数移动平均线优于简单移动平均线的一个主要地方。
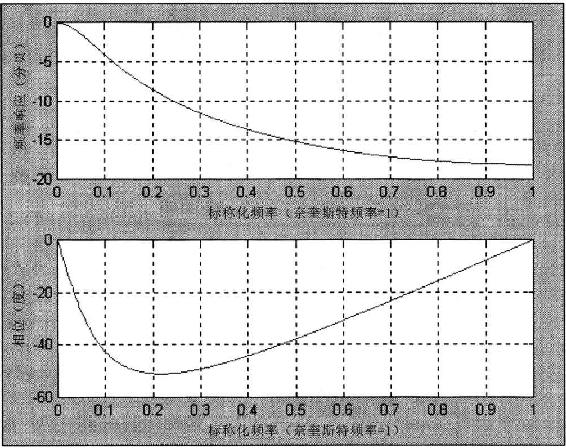
图4.8 α=0.222的指数移动平均线的频率和相位响应
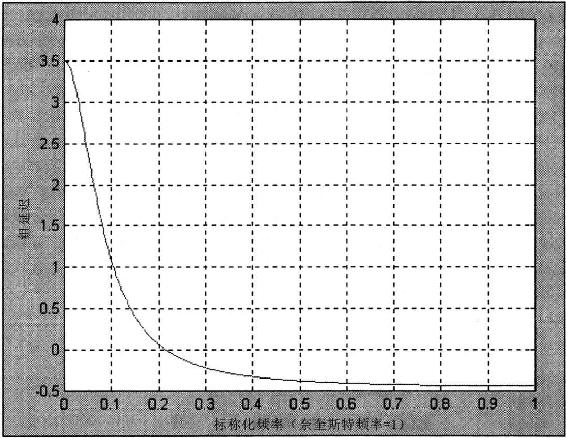
图4.9 α=0.222的指数移动平均线的组延迟响应
有理想特性的滤波器,被称为匹配滤波器。也就是说,它们的响应刚好匹配给定输入的波形和概率密度函数,任何没有和希望的波形一致的噪声都会被消除。当然,如果我们知道许多关于市场的波形,那么一开始就不需要滤波器。基本上来说,已经展示的低通滤波器的假设就是,我们想要的信号有一个相对低的频率,而噪声有较高的频率。因此,通过它们的频率特征,可以将我们想要的信号和噪声分开。但是,这个假设并不完全正确。
我们知道,价格有时可能会快速改变。这个快速改变说明一些短暂的高频组成波正在发挥作用。一些非线性的滤波器约翰·F.艾赫勒斯,《交易者的火箭科学》,约翰威利出版社,纽约,2001年,第17章和第18章。已经被设计出来,用来捕捉这些时间,然后消除高频噪声。考夫曼适应移动平均线(Kaufman’s Adaptive Moving Average,KAMA)和变指数动态平均线(VIDYA)滤波器可以通过应用观察到的波动性,改变指数移动平均线的α做到这一点。最大熵波谱分析适应移动平均线(MAMA)滤波器在应对突然的位相变化时移动了它的通带。艾赫勒斯滤波器是一个有限脉冲响应滤波器,其系数对应价格中波幅改变的剧烈程度。
一般来说,既然周期是对时间相对缓慢的变化参数,那么它们的最大熵波谱分析测量值,就对非线性滤波器几乎无法应用。因此,我们可以把这个讨论丢到一边。
•不考虑它们的公式,移动平均线的目的就是平滑所输入的数据。它们的用途就是在你想要的平滑的数量和你能够接受的延迟数量之间做权衡。最常见的移动平均线的特征如下:
延迟为(N-1)/2。
通带周期长度为2N。
窗口宽度的相位延迟为线性函数。
对交易重要的特定的周期长度可以使用对称加权系数。
延迟为(N-1)/3。
通带周期长度为2N。
对给定的延迟数量给出了最好的过滤。
窗口宽度的相位延迟是非线性函数。
α=1/(延迟+1)
α=2/(N+1),与简单移动平均线对比。
α和(1-α)的和必须为1。
通带周期长度为-2α/ln(1-α)=4α/(α·(2+α))。
由于卷积,位相延迟是非线性的。







