一个正弦量是由它的幅值、角频率和初相角（即三要素）所确定的，而在正弦电流电路中，电流和电压都是同频率的正弦量，所以在分析正弦电流电路时，只要计算出电流和电压的幅值和初相角就可以了。下面可以看到，一个正弦量的幅值和初相角可以用一个复数表示出来，这就是正弦量的相量表示法。
在介绍正弦量的相量表示法之前，先扼要地复习一下复数的几种表示形式及其运算。一个复数A有下面几种表示形式。
1.代数形式
图3-6所示为一复平面，横轴为实轴，用+1表示实单位；纵轴为虚轴，用+j表示虚单位。则一个复数便可用复平面上一个点表示。复数A还可用坐标原点O到点A的有向线段OA表示，OA叫做复数A的矢量。矢量长度用ρ表示，称为复数A的模；矢量与实轴正方向夹角θ，称为复数A的辐角。因此复数实部、虚部与模、辐角的关系如下：
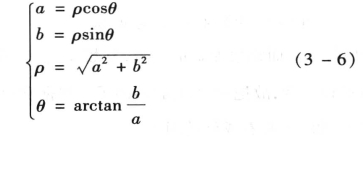
图3-6 复平面与复数
2.复数的三角形式
A =ρcosθ + jρsinθ =ρ （ cosθ + jsinθ）称为复数A的三角形式。
3.复数的指数形式
可把复数的三角形式变换为A =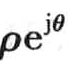 
，则A =
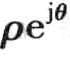称为复数的指数形式。
4.复数的极坐标形式
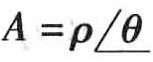称为复数的极坐标形式，它是复数的指数形式的简写形式。
复数的四则运算如下：
1.复数的加减运算
设复数A1 =a1 +jb1， A2 =a2 +jb2，则有
复数的加减运算可以按平行四边形法则在复平面上用作图法进行。图3-7（a）、（b）表示出复数A1 +A2和A1-A2的运算过程。
2.两个复数的乘除运算
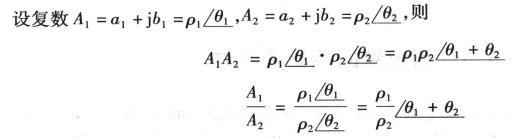
两个复数相乘和相除运算的几何意义如图3-7（c）、 （d）所示。
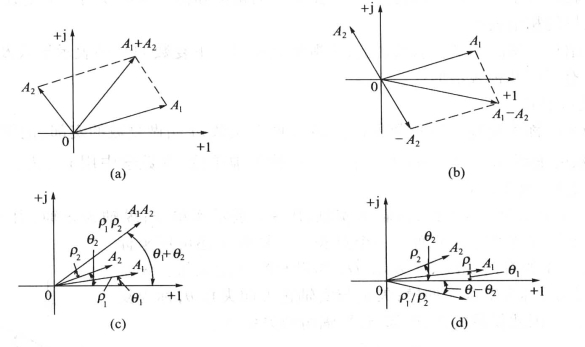
图3-7 复数A1和A2的四则运算
复数
是一个模等于1而辐角为φ的复数，复数
乘以ejφ等于把复数A逆时针旋转一个角度φ，而A的模不变，故把ejφ称为旋转因子。根据欧拉公式，不难看出
。因此±j和-1都看成旋转因子。
下面介绍正弦量的相量表示法。设有一正弦电流为
根据该正弦电流便可构造一个复指数函数Imej（ωt+φi）。由欧拉公式知
比较式（3-7）和式（3-8），可以看出复指数函数的虚部恰好是正弦电流i，即
式（3-9）表明，通过这种数学方法，得到了一实数域的正弦函数与一个复数域的复指数函数的一一对应关系。根据这种一一对应关系，可用复指数函数Imej（ωt+φi）表示正弦电流i。
由于正弦电流电路中各正弦量具有相同的角频率ω，每一个正弦量所对应的复指数函数中都含有旋转因子ejωte，因此可以把表达式Imej（ωt+φi） = Imejφiejωt中的ejωt省略掉，只用复常数Imejφi表示正弦电流i。Imejφi称为正弦电流i的幅值相量或最大值相量，记作
又由于实际中常用正弦电流的有效值，则把
复数可用复平面上矢量表示，相量是复数，也可用复平面上矢量表示。图3-8中画出了表示电流相量
=Imejφi的矢量，该矢量的长度及其与正实轴的夹角分别为Im和φi，此图形表示称为电流的相量图。需要指出的是：只有同频率正弦量的相量才能画在同一相量图中。
按式（3-9）也可直接作出相量图。复指数函数Imej（ωt+φi）在复平面上可用一矢量表示。因辐角（ωt+φi）是随时间匀速递增的，所以该矢量是绕坐标原点以角速度ω逆时针旋转的。因此复指数函数
及其在复平面上的图示都称为旋转相量。图3-9画出了旋转相量在t=0和t = t1的两个时刻的位置。式（3-9）表示复指数函数Ime（jωt+φi）的虚部等于正弦电流i，这一关系反映在图3-9中则为：旋转相量每一时刻在虚轴上的投影等于该时刻的正弦电流i。这是同一关系的两种表达方式，前者是解析表示，后者是几何表示。
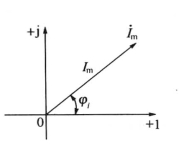
图3-8 相量图
图3-9 旋转相量与正弦波
例3-2 试写出正弦电流i1 =5sinωtA，i2=7sin（ωt +45°）A，i3 =10sin（ωt-120°）A的相量，并画出它们的相量图。
解 正弦电流i1、i2和i3的相量为
图3-10 例3-2图
其相量图示于图3-10。
例3-3 已知电压相量
。试写出它们所代表的正弦电压的瞬时值表达式，设角频率均为ω。
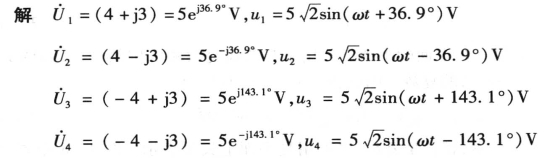
正弦量的下列运算可用对应的相量运算进行：
1.求同频率正弦量的代数和
设
，求i=i1 +i2…。由于同频率正弦量的代数和仍为一同频率的正弦量，即
，因此，根据式（3-12）有
由于上式对任何时间t都成立，故有
2.正弦量的微分
设
，则
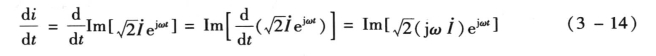
式（3-14）表明，正弦量的一阶导数仍为一同频率正弦量，其相量等于原正弦量的相量乘以jω。也就是说，正旋量的相量表示法，把实数域的正弦量的求导运算变换为复数域的相量与jω的相乘运算，即的相量为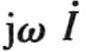
。
3.正弦量的积分
设正弦电流
，则
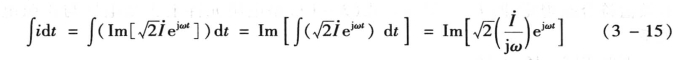
式（3-15）表明，正弦量的积分仍为同频率的正弦量，其相量等于原正弦量的相量除以jω。也就是说，正弦量的相量表示法，把实数域的正弦量的积分运算变换为复数域的相量与jω的相除运算。即∫idt的相量为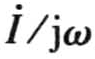
。
例3-4 设正弦电流
