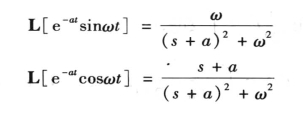拉普拉斯变换的性质很多，本节只介绍线性电路复频域分析中常用的几个基本性质。
1.线性性质
若L［f1（t）］ =F1（s），L［f2（t）］ =F2（s），a和b为两个任意常数，则有
即若干个原函数的线性组合的象函数，等于各原函数的象函数的线性组合。这一性质可利用拉普拉斯变换定义式（7-4）直接得到证明。
例7-1 利用线性性质求sinωt和cosωt的象函数。
解 因为
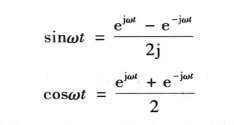
则
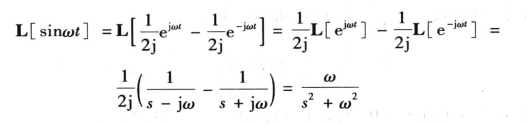
同理可得
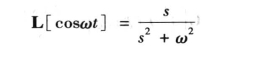
2.微分定理
若L［f（t）］=F（s），则
即时域中求导运算，对应于复频域中乘以s的运算，并减去原始值f（0-）。
应用分部积分法可得
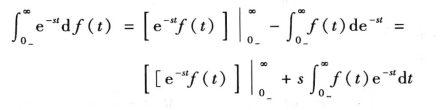
由于
是函数可进行拉普拉斯变换的条件，故有
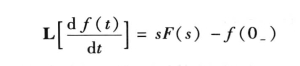
证毕。
微分定理推广至求原函数的二阶及二阶以上导数的象函数，即为
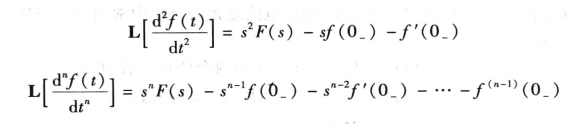
例7-2 已知L［δ（t）］=1，求δ（t）各阶导数的象函数。
解 由微分定理，可得δ（t）各阶导数的象函数为
3.积分定理
若L［f （t）］ =F（s），则
积分定理表明，时域中由0-到t的积分运算对应于复频域中除以s的运算。
由于t → ∞时，e-st→0；而t=0-时，
，所以
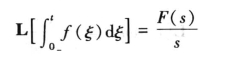
证毕。
例7-3 利用积分定理求
的象函数。
解 因为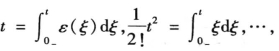
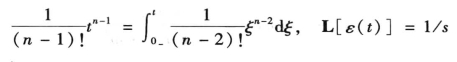
所以，由积分定理，有
4.时域位移定理
若L［f（t）］ =F（s），函数f（t）推迟t0出现而成为f（t-t0）ε（t-t0 ），则
上式中因为t ＜ t0时，ε（t-t0）=0，故把积分下限由0-换成
。令t′=tt-0，则t=t′+t0，dt=dt′，并且当t =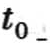 
时，t′=0-。所以
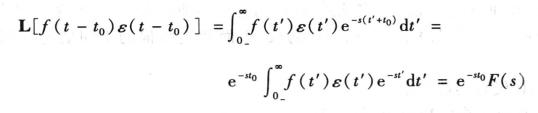
证毕。
例7-4 已知电压u（t）的波形如图7-1所示，求电压u（t）的象函数。
解 根据图7-1，写出电压u（t）的函数表达式
则根据线性性质和时域位移定理，得
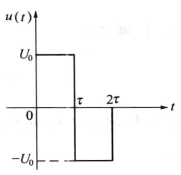
图7-1 电压波形
5.复频域位移定理
若L［f（t）］=F（s），则
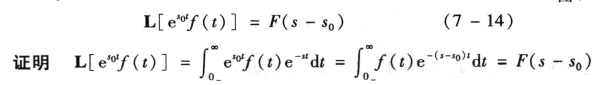
证毕。
例7-5 求函数e-at sinωt和e-atcosωt的象函数
解 由例7-1知
。根据复频域位移定理得
